|
Decision Support and Forecasting Center CEMI RAS |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Российские предприятия
Моделирование производственного потенциала фирмы c учетом факторов неэффективности и риска
М.Ю.Афанасьев, Н.В.Васильева
Работа поддержана РГНФ. Проект N 05-02-02174a.
Аннотация. Развивается методология оценки производственного потенциала фирмы, интегрирующая положения теории X-эффективности и концепцию стохастической граничной производственной функции. Построены модели, позволяющие учесть влияние идентифицируемых и не идентифицируемых сопутствующих факторов на оценку производственного потенциала. Проводится различие в подходах к его моделированию с учетом возможности управления факторами неэффективности. Дается сравнительный анализ построенных моделей с учетом ожидаемого объема производства, оценок неэффективности и риска воздействия сопутствующих факторов. Введение. Классическая концепция фирмы и методология оценки ее производственного потенциала длительное время развивалась в рамках технологической парадигмы, согласно которой результат труда полностью определяется факторами производственного процесса. Оценка производственного потенциала предприятия основывается на представлении о нем как о максимальном объеме производства за определенный период времени при фиксированном объеме использованных производственных факторов или как об объеме производства за период времени при наилучшем использовании факторов производства. Неоклассическое развитие взглядов на теорию фирмы привело к появлению производственной функции как инструмента описания производственного процесса . В упрощенной технологической конструкции «затраты-выпуск» производственная функция строится в виде детерминированной зависимости объема выпуска от факторов производственного процесса и может рассматриваться как модель производственного потенциала. Технологическая концепция фирмы выделяет основные факторы производства и абстрагируется от сопряженных факторов, характеризуя их действие как «прочие равные условия» /Маршалл, 1993/. Прочие условия, постоянно напоминающие о себе в эмпирических исследованиях, в конечном итоге вынуждают отказаться от технологической концепции при построении производственной функции. Этот переход прослеживается уже в работах /Робинсон, 1986/, и /Чемберлин, 1996/, рассматривавших качество продукции, уровень обслуживания, репутацию фирмы в качестве факторов конкуренции. Среди основных факторов производства начинают выделяться транспортные расходы, новые технологии, роль предпринимателя /Шумпетер, 1995/. Однако, на этом этапе развития теории фирмы не удается объяснить способность фирмы адаптироваться к изменениям, происходящим как внутри фирмы, так и за ее пределами. Наращивание объема производства остается возможным только в результате увеличения объема основных производственных факторов. Ограничения неоклассической теории привели в шестидесятые годы прошлого столетия к созданию новых моделей, развивавшихся в рамках институциональных теорий. Первые разработки, основанные на оптимизации трансакционных издержек фирмы /Коуз, 1995/ были дополнены уточнением роли специфических активов фирмы, инвестиций в человеческий капитал /Ульямсон, 1996/, /Ульямсон, 2003/. Было показано, что фирмы реагируют на факторы внешнего воздействия, которые могут иметь решающее значение в поведении фирмы. В предложенной О. Ульямсоном теории несовершенных контрактов отмечается невозможность предусмотреть поведение партнеров и, по существу, прослеживается ограниченность детерминистской концепции оценки производственного потенциала фирмы. Обуславливается необходимость учета риска и неопределенности. Этапным моментом в развитии теории фирмы и концепции ее производственного потенциала становиться появление теории X-эффективности Х. Лебенстайна /Lebenstein, 1966/. Он отметил, что основные факторы производства не определяют в полной мере его результат. Кроме основных, работают другие факторы, среди которых были особо выделены индивидуальная, внутрифирменная и внешняя мотивации. Эффективность труда во многом определяется отношением людей к труду, степенью их заинтересованности в наилучшем использовании имеющихся ресурсов. Неэффективная система оплаты труда, непредсказуемое вмешательство государства в деятельность фирмы, низкая мотивация являются факторами неэффективности, снижающими объем выпуска. Управление X-фактором, по мнению Лебенстайна, позволяет развивать производственный потенциал фирмы. Таким образом, производственный потенциал отражает возможности основных факторов производства. Конечной величины оценки полных возможностей на длительном интервале времени не существует, поскольку человек с его потребностями, как активная составляющая основных факторов производства, находится в постоянном развитии и совершенствовании. Но в любой достаточно малый момент времени оценка производственного потенциала может быть получена. Сейчас перечень сопутствующих факторов постоянно расширяется. Представляется полезным также введение признаков классификации факторов производственного процесса. Например, рассмотрение факторов различных уровней (мега-,макро-, мезо-, микроуровня) /Клейнер, 2004/, разделение их на управляемые и неуправляемые, внешние и внутренние. Самая высокая степень управляемости внутренними факторами на микроуровне. Менее управляемыми являются факторы макро-, мезосреды. Практически неуправляемы факторы мегасреды. Важной проблемой является идентификация сопутствующих факторов и получение количественных оценок результатов их воздействия. Сравнительно небольшой интерес к теории X-эффективности в течение почти тридцати лет объясняется отсутствием развитой методологии учета сопутствующих факторов. Один из путей преодоления этой проблемы возможен на основе синтеза теории X-эффективности и концепции стохастической граничной производственной функции. Появление граничной производственной функции было во многом предопределено понятием технологической эффективности производства, введенным Купманом и Дебрей. В шестидесятые годы прошедшего столетия появился непараметрический метод построения граничной производственной функции /Ferrier, Lovell, 1987/, основанный на моделях линейного программирования. В настоящее время реализация этого подхода нашла отражение в методологии DEA, которая позволяет строить граничные функции для многопродуктовых моделей и оценивать технологическую эффективность производства. Однако, при этом не удается получить функциональную зависимость объема выпуска от количества используемых факторов и описать причины, вызвавшие неэффективное использование ресурсов. Последнее обстоятельство ограничивает возможности применения непараметрических методов построения граничной производственной функции для идентификации и спецификации сопряженных факторов производства. Развитие параметрических методов привело к появлению стохастической граничной производственной функции, которая впервые была представлена независимо в работах /Aigner, Lovell, Schmidt,1977/ и /Meeusen, van den Broeck, 1977/. Стало ясно, что некоторые сопутствующие факторы оказывают случайное воздействие на производственный процесс, поэтому его результаты носят стохастический характер. Для того, чтобы учесть это, наряду с детерминированной составляющей, характеризующей действие основных факторов, производственная функция может включать случайную составляющую, моделирующую влияние сопутствующих факторов. Первая версия стохастической граничной производственной функции была построена в результате представления стохастической ошибки в виде двух составляющих, одна из которых имела усеченное в нуле нормальное распределение и позволяла моделировать воздействие факторов неэффективности. Позднее были ослаблены предположения относительно распределения составляющих, характеризующих ошибку наблюдения, введен фактор времени, построена модель функции издержек /Schmidt, Lovell, 1979/, /Battese, Coelli, Colby 1989/. Были проведены экспериментальные расчеты по оценке параметров стохастической граничной производственной функции методом максимального правдоподобия с использованием алгоритмов нелинейной оптимизации /Pitt, Lee,1981/, /Афанасьев, Скоков ,1984/. /Battese, Coelli, 1988/ и разработана программа FRONTIER для оценки параметров стохастической граничной производственной функции. /Coelli, 1992/, первые две версии которой позволяли оценивать параметры функции Кобба-Дугласа. На этом этапе развития стохастических методов параметризации граничной производственной функции последовательно решались две задачи. В начале строилась производственная функция и оценки неэффективности. Затем предпринимались попытка объяснить эту неэффективность. В работах /Kumbhakar, Ghosh, McGukin,1991/ и /Reifschneider, Stevenson,1991/ впервые было предложено объяснять неэффективность уже на этапе построения стохастической границы. Разработка версии 4.1 программы FRONTIER /Battese, Coelli, 1995/ открыла возможность для спецификации модели стохастической границы с учетом факторов неэффективности. Появился инструмент для идентификации и оценки X- фактора. Анализ сопутствующих факторов показывает, что их совокупность может быть разделена на две группы. Воздействие факторов первой группы может привести как к снижению, так и повышению объема производства и в целом характеризуется сбалансированным влиянием на производственный процесс. Результаты такого сбалансированного воздействия можно характеризовать как «белый шум». Примером факторов этой группы может служить солнечная геомагнитная активность. Независимо от того, какую плотность распределения имеет результат воздействия такого фактора, совокупное воздействие всех факторов этой группы характеризуется нормальным распределением. Эту первую группу факторов мы будем назвать сопутствующими факторами неуправляемого сбалансированного воздействия на производственный процесс или просто сбалансированными факторами. Факторы второй группы оказывают систематическое воздействие на производственный процесс, снижая его эффективность. Такие факторы обычно называются факторами неэффективности. К факторам неэффективности можно отнести отсутствие мотивации части персонала, его недостаточную квалификацию и т.д. Предлагаемые далее подходы к оценке производственного потенциала основываются на предположении, что фактический результат производства отличается от объема производства, соответствующего производственному потенциалу на величину, обусловленную воздействием факторов неэффективности. Наличие неопределенности в оценке результата производственного процесса позволяет говорить о риске воздействия сопутствующих факторов. Мы будем рассматривать риск как меру отклонения фактического результата производственного процесса от ожидаемого, независимо от того, в большую или меньшую сторону происходит это отклонение. В качестве количественной характеристики риска далее будет использоваться дисперсия. Можно предложить следующее определение производственного потенциала, учитывающее наличие неопределенности и неэффективности. Производственный потенциал - объем производства за определенный период времени при фиксированном объеме основных производственных факторов и отсутствии воздействия факторов неэффективности. В качестве модели производственного потенциала можно рассматривать зависимость результата производства от объема основных производственных факторов, учитывающую воздействие сопутствующих факторов при отсутствии факторов неэффективности. Построение модели производственного потенциала, соответствующее этому определению, предполагает возможность идентификации и устранения влияния всех факторов неэффективности. Такая модель отвечает представлению о наибольшем объеме выпуска в условиях ограниченности основных производственных факторов и наличии сбалансированного воздействия сопутствующих факторов. Составляющими модели могут служить детерминированная производственная функция, определяющая зависимость ожидаемого результата производства от объема основных производственных факторов, и стохастическая составляющая, характеризующая сбалансированное воздействие сопутствующих факторов. Метод наименьших квадратов [1], ставший почти универсальным в практической оценке параметров производственной функции, позволяет построить модель производственного потенциала в случае, если факторы неэффективности изначально отсутствуют или их влияние не проявляется. В этом случае ошибка (отклонение фактического объема производства от значения детерминированной производственной функции) имеет симметричное распределение. В принятой выше терминологии, асимметрия распределения ошибки свидетельствует о несбалансированном воздействии сопутствующих факторов, то есть о наличии воздействия факторов неэффективности. Тогда стохастическая составляющая производственной функции не может быть адекватно описана с помощью симметричного распределения и метод наименьших квадратов не позволяет получить хороших оценок параметров производственной функции. В этом случае можно применять концепцию граничной производственной функции, стохастическая составляющая которой учитывает, наряду с «белым шумом», воздействие факторов неэффективности и позволяет улучшить спецификацию модели производственного потенциала. Особое место в методологии оценки производственного потенциала занимает понятие эффективности производства. В соответствии с определением этого понятия в неоклассической теории производства, эффективность далее понимается как мера соответствия фактического результата производства максимально возможному при фиксированном объеме используемых основных производственных факторов. Здесь речь идет о технологической эффективности производства. Естественно, что максимально возможным мы будем считать результат производства, определяемый в соответствии с моделью производственного потенциала. В этой работе будут представлены модели производственного потенциала, отличающиеся способами идентификации факторов неэффективности. Для каждой модели получены экспериментальные оценки эффективности производства и риска воздействия сопутствующих факторов. Расчеты проводились для фирмы, работающей в Москве и специализирующейся на производстве и сбыте товаров хозяйственного назначения. Фирма имеет восемь производственных участков, размещенных в различных районах города. Каждый участок может предоставить покупателю любой товар, предлагаемый фирмой. Результат производственной деятельности- величина дохода в течение часа. В качестве характеристики производственного потенциала участка рассматривалась зависимость дохода производственно-торгового участка фирмы от объема трудозатрат и количества покупателей. Объем трудозатрат, измеряемый количеством обслуживающего персонала, находящегося на производственном участке и количество покупателей фиксировались ежечасно. Измерения проводились в течение двух недель работы фирмы на каждом из восьми ее производственных участков в течение десяти часов в день. Всего получены 1103 измерений. I. Модель производственного потенциала при сбалансированном воздействии сопутствующих факторов. Обозначения: i-индекс наблюдаемого события, i=1,…,N;
j – индекс основного производственного фактора, j=1,...,n.
Далее будем рассматривать
производственные функции вида,
иногда используя обозначение
Сбалансированность воздействия сопутствующих факторов не позволяет установить наличие неэффективности, поэтому в этих условиях может быть принята гипотеза об отсутствии факторов неэффективности. Тогда отличие фактического результата производства от ожидаемого описывается нормально распределенной случайной величиной. Модель 1 производственного потенциала.
При отсутствии неэффективности задача построения модели
производственного потенциала состоит в том, чтобы оценить параметры
зависимости
Тогда
Оценка параметров
Здесь β - вектор оцененных параметров производственной функции;
Если случайная величина
Однофакторная модель 1.1 производственного потенциала.
Результат производственной деятельности
Единственный основной производственный фактор – объем трудозатрат По результатам наблюдений методом наименьших квадратов построена следующая зависимость
Однако, в результате проверки гипотезы о нормальности распределения остатков, эта гипотеза была отвергнута. Более того, распределение остатков оказалось асимметричным. Поэтому, по результатам экспериментальных расчетов, функцию (2) нельзя рассматривать в качестве модели потенциала производственного участка фирмы. В этом случае естественно предположить, что на производственный процесс оказывают воздействие факторы, снижающие его эффективность. Двухфакторная модель 1.2 производственного потенциала.
Результат производственной деятельности
Рассматриваются два основных производственных фактора – объем
трудозатрат Методом наименьших квадратов построена зависимость
При проверке гопотезы о нормальности распределения остатков получена следующая диаграмма, где по оси абсцисс показано значение ошибки, а по оси ординат – число наблюдений.
В результате сравнения расчетного значения
При построении двухфакторной модели необходимо исключить мультиколинеарность, проявляющуюся в линейной корреляции основных факторов, так как ее наличие может привести к искажению полученных оценок. Для проверки гипотезы об отсутствии мультиколинеарности проанализируем коэффициент корреляции между логарифмированными значениями основных факторов. Его значение равно 0.05. Рассчитанная для него t-статистика равна 1.58, критическое значение на 5%-ом уровне значимости на два хвоста равна 1.64. Следовательно, на 5%-ом уровне значимости принимается гипотеза о незначимом отклонении коэффициента корреляции от нулевого значения. II. Модель производственного потенциала с необъясненной неэффективностью.
Модель 2 производственного потенциала с необъясненной
неэффективностью строится в предположении, что все факторы
неэффективности могут быть устранены, несмотря на то, что идентификация
этих факторов невозможна.
Здесь
Пусть
Оценка параметров
Задача оценки параметров производственной функции при необъясненной неэффективности:
Если значение
Модель производственного потенциала с неидентифицированными производственными факторами характеризуется стохастической производственной
функцией
Возможность достижения производственного потенциала предполагает, что все неидентифицированные факторы неэффективности могут быть устранены.
Располагая значениями ошибок
Оценки
при условиях
Если описывать технологическую эффективность факторов производства как
меру соответствия фактического результата производственного процесса
потенциально возможному, то количественной оценкой технологической
эффективности может служить величина
величина
Построим для нашего примера модель 2.1 производственного потенциала с одним основным производственным фактором. Методом максимального правдоподобия получены оценки параметров модели (3), приведенные в следующей таблице 1: Таблица 1
получаем
Используя оценки параметров, приведенные в таблице 1, получаем следующую модель производственного потенциала.
где
Построим теперь модель производственного потенциала для двух основных производственных факторов. Методом максимального правдоподобия получены оценки параметров модели (3), приведенные в следующей таблице 2. Таблица 2.
Тогда двухфакторная модель 2.2 производственного потенциала с необъясненной неэффективностью имеет вид
где III. Задача оценки производственного потенциала с объясняемой неэффективностью. Рассмотрим модель 3 производственного потенциала в предположении, что возможна идентификация факторов неэффективности. Взаимосвязь результата производства и объема используемых ресурсов представим в виде
Здесь
Задача оценки параметров производственной функции с объясняемой
неэффективностью имеет вид
Тогда модель производственного потенциала имеет вид
В экспериментальных расчетах была использована следующая функция неэффективности
где t1, t2, t3, t6 — булевы переменные, равные 1, если событие происходит в течение часа соответственно с 9.00 до 10.00, с 10.00 до 11.00, с 11.00 до 12.00 и с14.00 до 15.00 и равны нулю в противоположном случае; D1, D5, D6, D7 — булевы переменные, равные 1, если событие происходит в понедельник, пятницу, субботу и воскресенье соответственно, и равны нулю в противоположном случае; n0 — булева переменная, равная 1 для событий с нулевым объемом реализации. В нашей статистике имеется пять событий с нулевым объемом реализации. Объяснить их какими-либо закономерными процессами пока невозможно. Но влияние этих событий на построение границы эффективности есть. Для того, чтобы учесть это влияние, введена переменная n0; S — расстояние от центра города до производственного участка, измеренное в км; L18 — булева переменная, равная 1, если событие происходит при количестве персонала на производственном участке свыше 18 человек, равна нулю в противоположном случае; n1, n7, n8 — булевы переменные, равные 1, если событие происходит на 1-ом, 7-ом и 8-ом участках, иначе равны нулю; Pl — булева переменная, равная 1, если событие происходит на площади производственного участка свыше 1400 кв. м, иначе — равна нулю. Построим для нашего примера модель 3.1 производственного потенциала с одним основным производственным фактором. Результаты расчетов методом максимального правдоподобия для одного основного производственного фактора представлены в следующей таблице 3. Таблица 3.
* незначимые на 5% уровне. Используя оценки параметров, приведенные в таблице 3, получаем следующую модель производственного потенциала.
где
Риск неуправляемого воздействия при отсутствии факторов
неэффективности характеризуется величиной
В таблице 4 приведены оценки методом максимального правдоподобия параметров модели производственного потенциала с объясняемой неэффективностью для двух основных производственных факторов. Таблица 4.
* незначимые на 5% уровне. Проанализируем, что изменилось при введении в модель второго фактора. Для этого сравним полученные результаты с результатами, представленными в таблице 3. Во-первых, не изменилась эластичность по труду. Произошли незначительные изменения в коэффициентах при переменных, описывающих факторы неэффективности. Это говорит об их устойчивом влиянии на производственный процесс. Как было отмечено ранее, положительный знак перед коэффициентом показывает снижение эффективности. Соответствующий первому рабочему дню недели коэффициент при переменной (D1) изменил свое значение с 0.36 для однофакторной модели на 0.31 — в двухфакторной. Результат показал, что неэффективность снизилась. Следует сделать вывод о том, что часть неэффективности, которая имела место в однофакторной модели, объяснилась снижением количества потребителей в понедельник. В однофакторной модели не учитывалось то, что сокращение клиентов может привести к снижению объема реализации. В субботу эффективность снизилась. Коэффициент -0.37 — в однофакторной модели изменил значение на -0.33 — в двухфакторной. Разность этих коэффициентов объясняется увеличением количества клиентов в субботу. Однако, в субботу объем реализованной продукции по-прежнему выше в сравнении с другими днями недели (об этом говорит знак «-»), и это превышение уже не объясняется увеличением количества клиентов, а какими-то другими факторами. Возможно, для потребителей данной товарной продукции предпочтительнее делать свой выбор в приобретении того или иного товара именно в субботу. В двухфакторной модели возросла эффективность 8 участка (коэффициент n8 изменил значение с -0.18 до -0.22). Это говорит о том, что на данном участке более сильно проявляет себя фактор качества клиентов, т.е. увеличение посетителей ведет к большему увеличению реализации по сравнению с другими участками. Можно ожидать, что если мы построим для каждого участка в отдельности свою производственную функцию, то эластичность по фактору «количество клиентов» для 8-го участка будет самой высокой. Модель 3.2 производственного потенциала с двумя основными производственными факторами имеет вид
Риск неуправляемого воздействия при отсутствии факторов неэффективности
характеризуется величиной
В следующей таблице 5 приведены основные характеристики всех приведенных выше моделей производственного потенциала. Таблица 5.
В таблице 6 приведены формулы, описывающие детерминированные составляющие производственного производственного потенциала. Третий столбец таблицы содержит логарифмированные значения функции правдоподобия. Следует отметить, что значение функции правдоподобия значимо улучшается как при введении второго фактора, так и при объяснении неэффективности. Таблица 6.
На рисунке 1 изображены схематические изображения, характеризующие детерминированные составляющие моделей производственного потенциала с одним основным фактором производства. Детерминированная составляющая модели 1.1, оцененная с помощью метода наименьших квадратов, обозначена I и на рисунке занимает нижнее положение. Детерминированная составляющая модели 2.1, обозначенная как кривая II, занимает среднее положение. Детерминированная составляющая модели 3.1, обозначенная как кривая III, занимает верхнее положение. Как видно из рисунка, уточнение описания случайной величины, характеризующей воздействие факторов неэффективности, приводит к тому, что скорость роста детерминированных составляющих однофакторных моделей производственного потенциала увеличивается. IV. Оценка производственного потенциала с учетом возможности управления факторами неэффективности. Достижение производственного потенциала, оцененного с помощью моделей 2.1, 2.2, 3.1 и 3.2, предполагает возможность устранения влияния всех факторов неэффективности. Поэтому производственный потенциал, оцененный с помощью этих моделей, может оказаться идеализированной конструкцией, не имеющей основы реального воплощения. Факторы неэффективности могут быть управляемыми и неуправляемыми. При этом управляемыми следует считать такие факторы неэффективности, которые, во-первых, можно идентифицировать и , во-вторых, воздействие которых можно полностью или частично устранить А так как не все факторы неэффективности являются управляемыми, то построенные выше модели естественно рассматривать как оценки производственного потенциала сверху. В попытке более точной оценки можно исходить из того, что фактический результат производственного процесса может быть улучшен лишь за счет воздействия на управляемые факторы неэффективности. Тогда оценка производственного потенциала предприятия превышает фактически наблюдаемый результат производства на величину, определяемую воздействием управляемых факторов неэффективности. Исходя из этого, можно предложить следующее определение производственного потенциала, учитывающее возможность управления факторами неэффективности. Определение 2. Производственный потенциал – объем производства за определенный период времени при фиксированном объеме основных производственных факторов и отсутствии воздействия управляемых факторов неэффективности. Тогда в качестве модели производственного потенциала можно рассматривать зависимость результата производства от объема основных производственных факторов, учитывающую воздействие неуправляемых сопутствующих факторов. Для того, чтобы построить модель производственного потенциала, соответствующую этому определению, необходимо, во-первых, выявить факторы неэффективности, во – вторых, разделить их на управляемые и неуправляемые. Тогда модель производственного потенциала будет включать детерминированную составляющую, определяющую зависимость результата производства от объема основных производственных факторов и стохастическую составляющую, характеризующую совокупное воздействие сбалансированных факторов и неуправляемых факторов неэффективности. Производственный потенциал, построенный в соответствии с определением 2, достижим в той мере, в которой может быть устранено воздействие управляемых факторов неэффективности. Даже в том случае, если удается идентифицировать факторы неэффективности, все они могут оказаться неуправляемыми. Используя оценки параметров, приведенные в таблице 3, получаем однофакторную модель 4.1 производственного потенциала, соответствующую определению 2 в предположении, что все идентифицированные факторы неэффективности являются неуправляемыми:
m =15.
Пусть
Двухфакторная модель 4.2 производственного потенциала, соответствующая определению 2 в предположении, что все идентифицированные факторы неэффективности являются неуправляемыми, строится по данным таблицы 4 и имеет вид
Риск воздействия неуправляемых сопутствующих факторов характеризуется величиной
Рассмотрим модель производственного потенциала, соответствующую определению 2 в предположении, что некоторые идентифицированные факторы неэффективности являются управляемыми. Пусть
компоненты
компоненты
Введем обозначения
Тогда
Воздействуя на управляемые факторы неэффективности, можно изменять
значение величины
где ,
Устраняя воздействие управляемых факторов неэффективности, мы переходим от
случайной величины
Авторы признательны А.Д.Сластникову, давшему полезные
рекомендации по улучшению работы и предложения по альтернативному
способу моделирования воздействия неуправляемых факторов неэффективности. Рисунок 2.
Однофакторная модель 4.3 производственного потенциала, соответствующая определению 2 в предположении, что некоторые факторы неэффективности являются управляемыми, строится по данным таблицы 3. Предположим, что первые 14 из 15 идентифицированных факторов неэффективности фирма относит к категории неуправляемых, а 15-ый фактор отнесем к категории управляемых. Например, снижение эффективности, объясняемое большой площадью производственного участка можно устранить, сдав часть площади в аренду. Тогда, используя оценки параметров, приведенные в таблице 2, получаем следующую модель производственного потенциала.
Риск воздействия неуправляемых сопутствующих факторов характеризуется величиной
где
Выводы
Список литературы:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Контакты: ЦЭМИ РАН 117418, Москва, Нахимовский проспект, 47, комната 1110 |
|
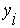 -
результат производственной деятельности, соответствующий наблюдению
-
результат производственной деятельности, соответствующий наблюдению
 -
объем фактора производства
-
объем фактора производства 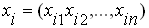 -
вектор объемов факторов производства, соответствующий наблюдению
-
вектор объемов факторов производства, соответствующий наблюдению 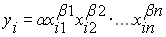
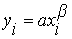 ,
где
,
где
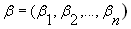
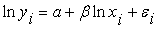 .
.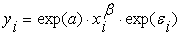
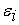
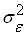 ,
то есть
,
то есть
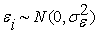 .
.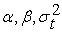 может
быть выполнена методом наименьших квадратов. Такой подход предполагает
использование методов анализа панельных данных, предусматривающих
тестирование наличия фиксированных или случайных эффектов применения ОМНК. Эти исследования в работе не приводятся. Рассматривается лишь
гипотеза о нормальности распределения остатков
может
быть выполнена методом наименьших квадратов. Такой подход предполагает
использование методов анализа панельных данных, предусматривающих
тестирование наличия фиксированных или случайных эффектов применения ОМНК. Эти исследования в работе не приводятся. Рассматривается лишь
гипотеза о нормальности распределения остатков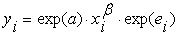
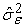
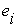
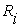 ,
соответствующей наблюдению i.
,
соответствующей наблюдению i.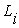 ,
соответствующей наблюдению i,
,
соответствующей наблюдению i,
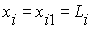 .
.

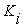 , соответствующие наблюдению i,
, соответствующие наблюдению i,
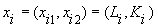 .
.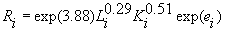 ,
,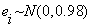
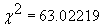 с критическим 22.36 на 5%-ом уровне значимости, гипотеза о нормальности
распределения остатков может быть отклонена.
с критическим 22.36 на 5%-ом уровне значимости, гипотеза о нормальности
распределения остатков может быть отклонена. ,
,
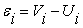
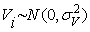
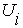 ;
;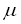
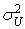 ,
далее
,
далее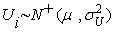 , используемая для идентификации систематического воздействия на
производственный процесс всей совокупности факторов, снижающих его
эффективность;
, используемая для идентификации систематического воздействия на
производственный процесс всей совокупности факторов, снижающих его
эффективность;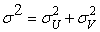 -
«полная» дисперсия;
-
«полная» дисперсия;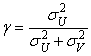
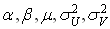 может быть выполнена методом максимального правдоподобия, описанным в /Battese,
Coelli, 1992/, и реализованным в программе FRONTIER 2.0. /Coelli, 1992/
или в ее более поздней версии FRONTIER 4.1. Этот метод позволяет
получить несмещенные оценки параметров, имеющие наименьшую дисперсию.
может быть выполнена методом максимального правдоподобия, описанным в /Battese,
Coelli, 1992/, и реализованным в программе FRONTIER 2.0. /Coelli, 1992/
или в ее более поздней версии FRONTIER 4.1. Этот метод позволяет
получить несмещенные оценки параметров, имеющие наименьшую дисперсию.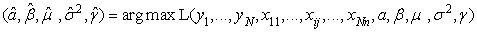
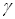 параметра асимметрии значимо не отличается от нуля, то
можно сделать вывод об отсутствии факторов неэффективности, так как
дисперсию
параметра асимметрии значимо не отличается от нуля, то
можно сделать вывод об отсутствии факторов неэффективности, так как
дисперсию
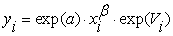
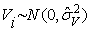 .
.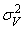 , можно для
каждого наблюдения i получить оценки составляющей
, можно для
каждого наблюдения i получить оценки составляющей
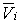 , объясняемой
воздействием сбалансированных факторов и составляющей
, объясняемой
воздействием сбалансированных факторов и составляющей
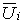 , объясняемой
воздействием факторов неэффективности. Один из возможных подходов
разделения ошибки на составляющие описан в работе /Jondrow, Lovell,
Materov, Schmidt, 1982/.
, объясняемой
воздействием факторов неэффективности. Один из возможных подходов
разделения ошибки на составляющие описан в работе /Jondrow, Lovell,
Materov, Schmidt, 1982/. 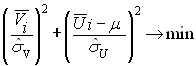
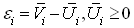
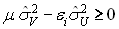 , то
, то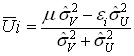
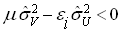
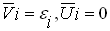
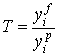
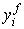
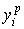 - потенциально возможный. Так как
фактический объем производства равен
- потенциально возможный. Так как
фактический объем производства равен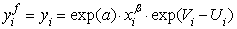 , а потенциально возможный
, а потенциально возможный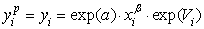 , то
мерой технологической эффективности может служить
, то
мерой технологической эффективности может служить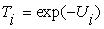 . С учетом
этого, величину
. С учетом
этого, величину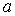
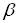
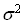
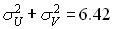
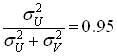 ;
; 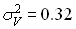 ,
,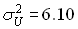 .
.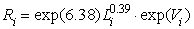 ,
, 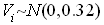 .
Риск неуправляемых воздействий при отсутствии факторов
неэффективности характеризуется величиной
.
Риск неуправляемых воздействий при отсутствии факторов
неэффективности характеризуется величиной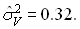
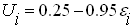
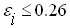 , иначе
, иначе
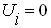 .
.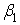
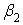
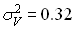 ,
,
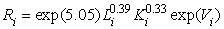 ,
,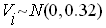 .
.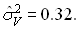
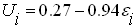
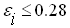
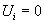 .
.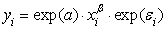
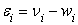
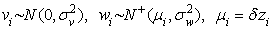
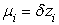
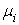
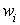
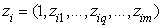
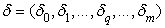
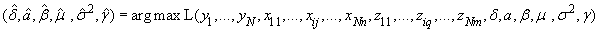
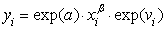 ,
,
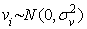 .
.
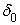
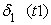
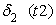
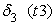
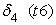
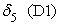
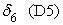
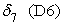
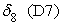
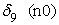
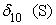
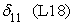
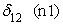
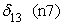
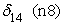
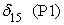
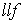
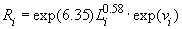 , (6)
, (6)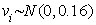 .
Значение дисперсии
.
Значение дисперсии
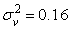 получено из решения системы уравнений
получено из решения системы уравнений 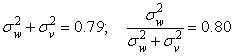
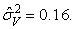 Отметим, что этот риск снизился по сравнению с моделью 2.1. По аналогии
с тем, как были получены оценки неэффективности в модели 2.1, можно
оценить неэффективность в модели 3.1:
Отметим, что этот риск снизился по сравнению с моделью 2.1. По аналогии
с тем, как были получены оценки неэффективности в модели 2.1, можно
оценить неэффективность в модели 3.1: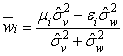 если
если
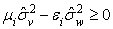
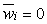
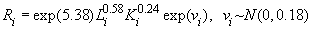
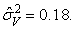
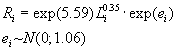
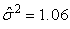
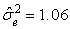
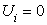
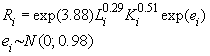
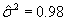
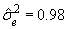
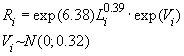
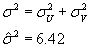
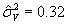
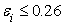 ,
то
,
то 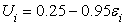
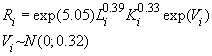
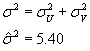
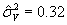
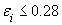 ,
то
,
то 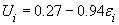
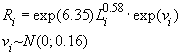
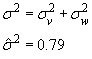
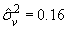
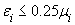 ,
то
,
то 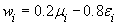

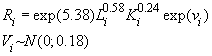
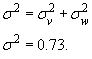
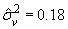
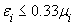 ,
то
,
то 


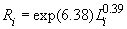
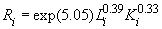
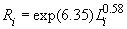
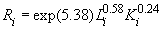
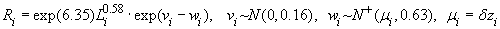
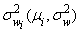 -
дисперсия случайной величины
-
дисперсия случайной величины
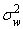
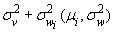 .
Оценка неэффективности для каждого наблюдения равна нулю.
.
Оценка неэффективности для каждого наблюдения равна нулю.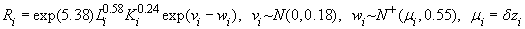
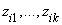
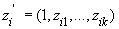
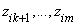
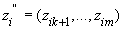
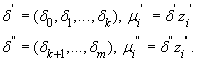
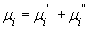 .
.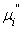 .
Пусть
.
Пусть
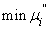 -
минимальное значение величины
-
минимальное значение величины
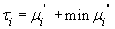 .
Тогда модель производственного потенциала имеет вид
.
Тогда модель производственного потенциала имеет вид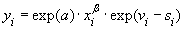
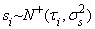 ,
,
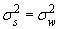 .
.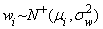 ,
моделирующей воздействие всех факторов неэффективности к случайной
величине
,
моделирующей воздействие всех факторов неэффективности к случайной
величине
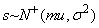
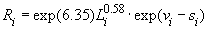
 , где
, где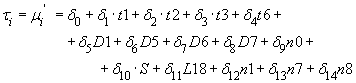 (7)
(7)  ,
где
,
где
 -
дисперсия случайной величины
-
дисперсия случайной величины
 .
.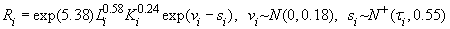
 -
определяется по формуле (7) на основании данных таблицы 4. Риск
воздействия неуправляемых сопутствующих факторов характеризуется
величиной
-
определяется по формуле (7) на основании данных таблицы 4. Риск
воздействия неуправляемых сопутствующих факторов характеризуется
величиной