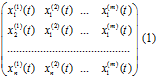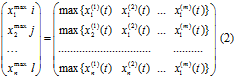|
Decision Support and Forecasting Center CEMI RAS |
||
|
|
Эконометрическая теория и практика
О классификации регионов России в пространстве компонент - валовых добавленных стоимостей, валового регионального продукта.*
А.Н. Березняцкий.
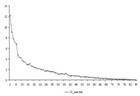
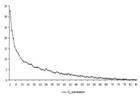
В ряде научно-практических задач необходимо произвести разбиение некоторой группы объектов на классы. Это может быть как самодостаточная задача, на выходе которой нас интересует, каким образом группируются объекты, так и вспомогательная, когда классификация необходима для решения некоторой другой задачи. В рамках стратегии пространственного развития России разрабатывается класс моделей социально-экономической динамики, для статистической верификации которых требуется разбиение регионов России на однородные в некотором смысле группы. В этой работе представлен один из возможных подходов к решению этой задачи: разбиение регионов по схожим «хозяйствующим портретам». Существует два принципиально разных подхода к классификации: экспертный и подход на основе методов многомерного статистического анализа. В первом варианте регионы анализируются экспертами с соответствующей подготовкой и по ряду количественно-качественных признаков относятся к тому или иному кластеру. В этом отношении следует отметить работы школы регионалистики под руководством Зубаревич Н.В. (см. к примеру, (Зубаревич, 2010)). Во втором подходе разбиение регионов на классы определяется исключительно количественным анализом в рамках выбранного метода (алгоритма) классификации (Айвазян и др., 1974, 1989), (Everitt et al, 2011). Далее мы рассмотрим количественный подход к классификации. На входе задачи используются данные Росстата по валовому региональному продукту и его компонентам в виде валовых добавленных стоимостей (ЕМИСС, 2017). При этом вектор параметров, характеризующих регион, может формироваться в соответствии с различной методологией. Традиционно используется подход, в котором вектор состоит из компонент-долей валовых добавленных стоимостей в валовом региональном продукте региона. Так называемая концепция «абсолютной специализации». Далее будет представлен пример методики в отношении концепции «относительной специализации», когда вектор формируется из компонент-долей валовых добавленных стоимостей региона в соответствующих общероссийских. Таким образом, делается акцент на роли региона в производственной структуре российской экономики и исключается влияние изменения цен на производственную структуру региона. В отношении данных имеется скудный объем информации: заранее неизвестно количество классов, статистические свойства данных (законы распределения, моменты) не заданы. В этом случае наиболее распространенными методами кластеризации являются разновидности метода К-средних и иерархические процедуры (Айвазян и др., 1989), (Mirkin, 2005), (Wu, 2012). Для реализации алгоритма К-средних требуется информация о количестве классов, которой мы не обладаем. И все-таки алгоритм может быть полезен и в этом случае. Дело в том, что в случае с регионами мы фактически имеем дело с генеральной совокупностью, а не с выборкой данных: множество регионов конечно и в нашем распоряжении данные о всех регионах. Таким образом, потенциальное количество классов ограничено сверху количеством регионов. Величина эта относительно небольшая и даже с учетом размерности вектора параметров вполне под силу современной среднестатистической вычислительной машине. Анализ поведения оптимальных значений функционала качества разбиения при переборе числа кластеров от единицы до количества регионов может дать информацию о потенциальном «истинном» количестве классов. Ожидается, что по мере приближения к «истинному» количеству кластеров будет происходить резкое уменьшение оптимальных значений функционала. В дальнейшем должно происходить равномерное снижение оптимальных значений по мере увеличения количества кластеров (в силу построения алгоритма). Результаты прогона алгоритма в MATLAB представлены на рис. 1.
Рис. 1. Динамика оптимальных значений функционала качества разбиения алгоритма К-средних для всех возможных значений количества кластеров k. Как видно из рис. 1, переход с резкого снижения оптимальных значений функционала к пологому происходит в районе равному 10-12. Зная ориентировочное значение числа k, можно применить алгоритм К-средних для окончательной классификации. Оценить потенциальное количество классов можно и несколько иным способом. Далее приводится схема эвристического алгоритма. Основная идея следующая: потенциальное количество классов эквивалентно числу видов экономической деятельности по ОКВЭД. Регион относится к конкретному классу-виду экономической деятельности по максимальному значению доли вида экономической деятельности в общероссийской для заданного региона. Эвристический алгоритм разбиения. 1. шаг. На входе матрица размера nxm, где n – количество объектов (регионов России), m – количество видов экономической деятельности (ВДС), t – период времени регистрации данных:
2. шаг. Максимальное количество классов известно и совпадает с
количеством видов экономической деятельности. Вычисляется максимальное
значение в каждой из строк матрицы (1), фиксируется координата
максимального значения в строке:
3. шаг. Объект относится к заданному классу по координате в строке максимального значения. Эвристический алгоритм дал оценку числа классов k равной 12, что вполне согласуется с результатами экспериментов по методу К-средних. С целью анализа качества алгоритма разбиения можно проверить траектории кластеров во времени. Предполагается неизменность структуры экономики России в кратко и среднесрочной перспективе, таким образом, и состав кластеров должен быть неизменен. Результат применения алгоритма к данным из (ЕМИСС, 2017), реализованного в MATLAB, приводится ниже. Прогон алгоритма проводился для всех t:
Необходимо отметить, что в данной методике рассмотрен максимально жесткий вариант использования методов классификации: рассматривается полный набор регионов и полный набор видов экономической деятельности. В результате экспертного анализа количество регионов может быть предварительно уменьшено, отдельные виды деятельности могут быть сгруппированы с целью снижения размерности пространства (см. Айвазян и др., 2016).
Рис. 2. Классификация регионов России в пространстве компонент – валовых
добавленных стоимостей, траектории кластеров (приведены выборочно 2
кластера; цвет обозначает тип класса)
* Тезисы доклада на XI-й Международной конференции "Применение многомерного статистического анализа в экономике и оценке качества".
|
|
|
Контакты: ЦЭМИ РАН 117418, Москва, Нахимовский проспект, 47, комната 1110 |
|