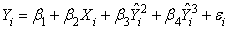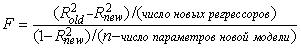|
Decision Support and Forecasting Center CEMI RAS |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Прогнозы
О среднесрочных тенденциях в динамике производства товаров и услуг в России
Бродский Б.Е.
Сложившаяся в России практика прогнозирования индексов физического объема производства в основных секторах и отраслях экономики ориентирована, по преимуществу, на экспертные оценки и «балансовые модели». Гораздо меньшее внимание уделяется разработке динамических регрессионных моделей, в которых оцениваются эластичности индексов физического объема производства по отношению к основным влияющим факторам: показателям внешнеэкономической конъюнктуры на рынках экспортируемых товаров, государственной ценовой политики в отраслях естественных монополий, факторам валютного курса, инфляционных ожиданий, кредитно-денежной и налоговой политики. В данной работе использована методология коинтеграционного моделирования индексов физического объема производства (ИФО), которая позволяет оценивать среднесрочные и краткосрочные тенденции в динамике ИФО, а также коэффициенты эластичности ИФО по отношению к основным влияющим факторам. Согласно результатам проведенных эконометрических исследований, к числу основных факторов, определяющих динамику производства в основных секторах и отраслях российской экономики в среднесрочной перспективе, следует отнести:
Эти выводы были получены на основе эконометрического моделирования динамики индексов физического объема производства (ИФО) в период 1994(1)-2004(4), измеренных с квартальным интервалом. Целью эконометрического моделирования была оценка эластичностей индексов физического объема производства по основным влияющим факторам, а также построение эконометрических зависимостей, пригодных для прогнозирования динамики ИФО на среднесрочный период. Промышленность в целом Для анализа среднесрочных тенденций в динамике промышленного производства будем основываться на выводах следующих теоретических работ, посвященных анализу факторов, влияющих на общую макроэкономическую ситуацию и на среднесрочные тенденции в динамике промышленного выпуска в России (Айвазян, Бродский (2005), Бродский (2005)). К числу этих факторов следует, в первую очередь, отнести:
Коинтеграционная модель, описывающая устойчивые среднесрочные тенденции в динамике промышленного производства в России с учетом отмеченных факторов, полученная на основе квартальных данных за период 1997(1)-2004(4), имеет следующий вид:
где числа в скобках во второй строке являются значениями t-статистики для соответствующих коэффициентов;
Полученная коинтеграционная зависимость позволяет сделать следующие выводы:
Помимо коинтеграционной модели, описывающей устойчивые среднесрочные тенденции в динамике промышленного производства в России, была исследована модель коррекции ошибок, позволяющая учитывать краткосрочные эффекты, влияющие на динамику промышленного производства, например, сезонные факторы, эффект кризиса 1998 г. и др. Для построения модели коррекции ошибок использовался метод Энгеля-Грейнджера, предусматривающий включение переменной регрессионных остатков коинтеграционной модели в качестве объясняющего фактора для модели коррекции ошибок. Полученная модель коррекции ошибок для базового индекса промышленного производства имеет вид:
Эта модель позволяет оценить
краткосрочный коэффициент эластичности индекса промышленного
производства по фактору
На динамику промышленного производства в России существенное влияние оказывают сезонные факторы: сезонный спад производства в первом и втором квартале составляет 5% и 2% соответственно, в третьем квартале наблюдается сезонный рост индекса на 3%. Помимо вышеперечисленных факторов, в период после кризиса 1998 г. в России на динамику промышленного производства существенный позитивный эффект оказал фактор роста монетизации финансовых взаиморасчетов между предприятиями s1999p1: краткосрочная эластичность индекса промышленного производства по этому фактору составляет 0.03. Далее приведены статистические показатели качества полученных зависимостей. Отметим, что всюду далее l обозначает log, f (fitted) -модельный (подобранный) ряд D – оператор взятия первой разности, R – ряд регрессионных «остатков». Подробное описание статистических тестов и используемых в них обозначений приведено в Приложении. Моделирование показателя log(Ind) методом OLS Выборка данных: 1997 (1) - 2004 (4)
Моделирование показателя Dlog(Ind) методом OLS Выборка данных: 1997 (2) - 2004 (4)
* - значима на 5% уровне ошибки выражение в квадратных скобках – это вероятность того, что данная статистика равна нулю
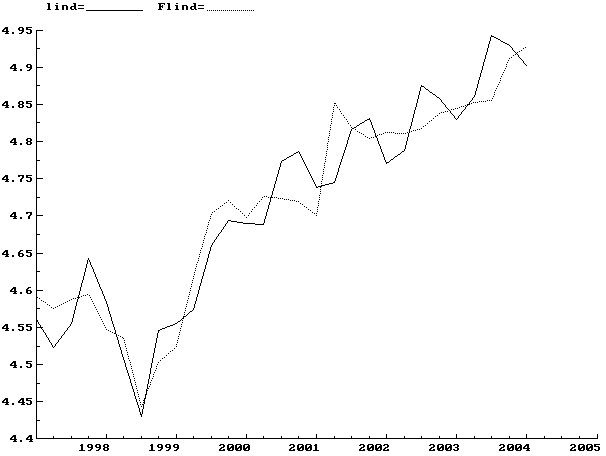
На Рис. 1 приведен график исследуемого показателя и его расчета по данной модели.
Рис. 1
Все
статистические тесты (AR –
автокорреляция остатков,
ARCH тест,
Normality нормальность остатков,
Xi2 – гетероскедастичность,
RESET
тест) подтвердили приемлемое
качество полученной зависимости.
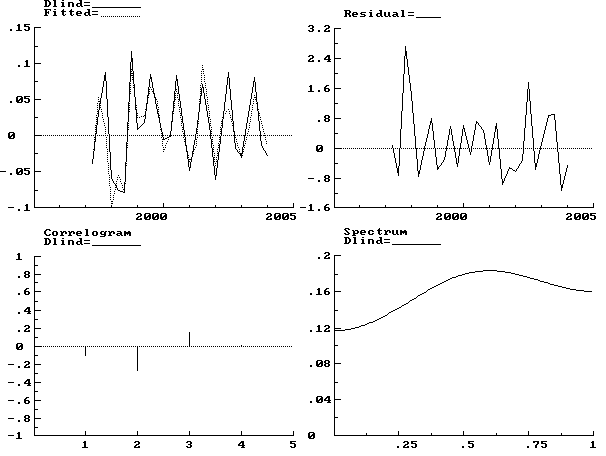
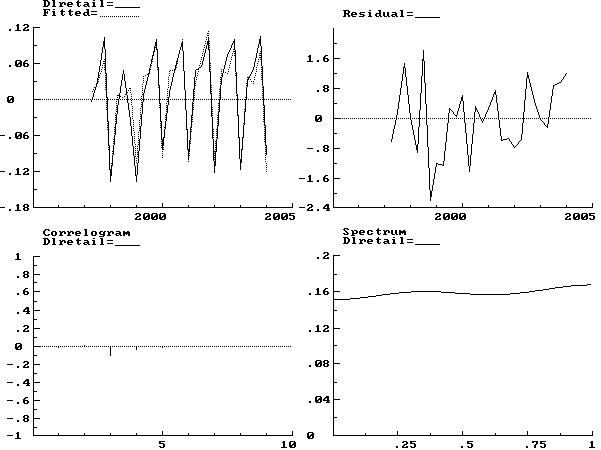
На Рис. 2 приведены следующие
графики:
Рис. 2 Строительство Полученная коинтеграционная модель для индекса физического объема строительных работ имеет следующий вид:
Из этой модели следует, что основными факторами, влияющими на динамику физического объема строительных работ в среднесрочной перспективе, являются реальные доходы населения (rinc) и индекс тарифной политики естественных монополий (rmon). Эти выводы объясняются тем, что реальные доходы населения являются важнейшим фактором макроэкономической конъюнктуры, определяющим агрегированный спрос на строительные работы (включая строительство жилых домов). Индекс тарифной политики в отраслях естественных монополий влияет на издержки строительных компаний (через закупки строительных материалов, услуги транспорта и др.). Коэффициент эластичности индекса производства в строительстве по фактору реальных доходов населения равен 1.11. Это означает, что рост реальных доходов населения на 1% приводит к увеличению реального объема строительных работ на 1.11% в среднесрочной перспективе. Коэффициент эластичности индекса производства в строительстве по индексу тарифной политики в отраслях естественных монополий равен -0.44. Это означает, что опережающий индекса тарифной политики естественных монополий на 1% ведет к спаду реального объема строительного производства на 0.44%. Сезонные факторы оказывают существенное влияние на динамику строительного производства: сезонный спад в первом квартале достигает 30% и компенсируется сезонным ростом на 18% во втором и 17% в третьем квартале. Моделирование показателя lconstr методом OLS Выборка данных: 1997 (1) - 2004 (3)
Моделирование показателя Dlconstr методом OLS Выборка данных: 1997 (2) - 2004 (3)
** означает, что гипотеза значима на 1% уровне ошибки выражение в квадратных скобках – это вероятность того, что данная статистика равна нулю
Сельское хозяйство Полученная коинтеграционная модель для индекса физического объема сельскохозяйственного производства на интервале квартальных данных 1997(1)-2004(4) имеет следующий вид:
Из этой модели следует, что основными факторами, влияющими на динамику сельскохозяйственного производства в среднесрочной перспективе, являются: реальный обменный курс (er), индекс тарифной политики в отраслях естественных монополий (rmon), налоговые факторы (s2001p2). Коэффициент эластичности индекса физического объема сельскохозяйственного производства по реальному обменному курсу (доллара) является статистически значимой отрицательной величиной (-0.27). Это объясняется тем, что экономический рост в 1997-2004 гг. в России происходил на фоне укрепления рубля в реальном выражении, вызванным высоким уровнем мировых цен на нефть и притоком «нефтедолларов» в страну, вызвавшим бурный рост реальных доходов населения и расширение совокупного спроса на сельскохозяйственную продукцию. При этом укрепление рубля в реальном выражении замедляет процесс углубления дифференциации населения по доходам и способствует расширению спроса именно на отечественную сельскохозяйственную продукцию. Напротив, динамика индекса тарифной политики в отраслях естественных монополий отражает тенденции на стороне предложения сельскохозяйственной продукции, влияя на издержки предприятий агрокомплекса: коэффициент эластичности реального объема сельскохозяйственного производства по фактору rmon равен -0.16 по среднесрочной тенденции. Это означает, что каждый дополнительный процент опережающего роста тарифов естественных монополий по сравнению с инфляцией на потребительском рынке ведет к снижению реального объема сельскохозяйственного производства на 0.16%. Сезонные факторы чрезвычайно существенны в динамике сельскохозяйственного производства в России: в первом квартале сезонный спад достигает 36% по сравнению с предыдущим кварталом, однако в третьем квартале он компенсируется сезонным ростом в 56%. Моделирование показателя Rlagro методом OLS Выборка данных: 1997 (1) - 2004 (4)
выражение в квадратных скобках – это вероятность того, что данная статистика равна нулю
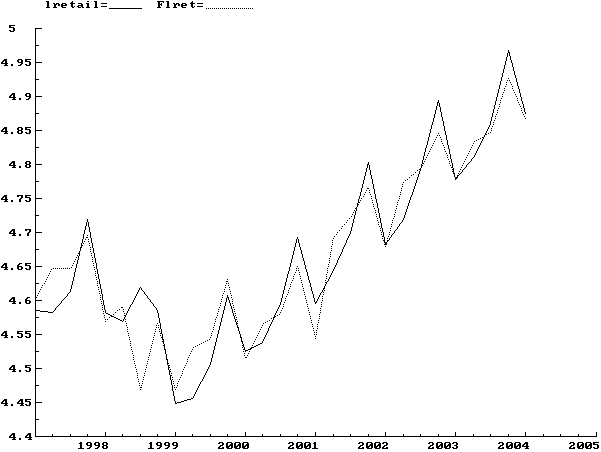
Розничная торговля Полученная эконометрическая модель коррекции ошибок для индекса розничной торговли с использованием квартальных данных Госкомстата за период 1997(1)-2004(4) имеет следующий вид:
Эта модель описывает как среднесрочные, так и краткосрочные тенденции в динамике индекса розничной торговли. К основным факторам, влияющим на динамику индекса розничной торговли в среднесрочной перспективе, следует отнести: реальные доходы населения (rinc), индекс тарифной политики в отраслях естественных монополий (rmon), налоговые факторы (s2001p2). Коэффициент эластичности индекса объема розничной торговли по фактору реальных доходов населения составляет 0.55. Это означает, что каждый дополнительный процент прироста реальных доходов населения приводит к возрастанию индекса объема розничной торговли на 0.55% по среднесрочной тенденции. Снижение налогового бремени и, в частности, снижение эффективной ставки ЕСН оказывают положительное влияние на рост реального объема розничной торговли: среднесрочный коэффициент эластичности индекса объема розничной торговли по фактору s2001p2 составляет 0.07. Помимо этих факторов, оказывающих преимущественное влияние на формирование среднесрочных тенденций в динамике индекса розничной торговли, можно выделить следующие факторы, влияющие на краткосрочные тенденции в динамике розничной торговли: реальная заработная плата (краткосрочный коэффициент эластичности по фактору реальной заработной платы составляет 0.25), сезонные факторы (сезонный спад объема розничной торговли в первом квартале достигает 15% по сравнению с предыдущим кварталом), укрепление денежных форм взаиморасчетов между предприятиями (фактор s1999p1). Моделирование показателя lretail методом OLS Выборка данных: 1997 (1) - 2004 (3)
Моделирование показателя Dlretail методом OLS Выборка данных: 1997 (2) - 2004 (4)
выражение в квадратных скобках – это вероятность того, что данная статистика равна нулю
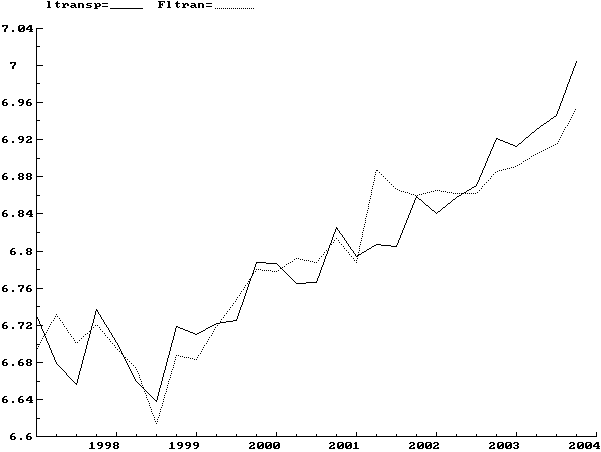
Транспорт Полученная коинтеграционная зависимость для показателя динамики коммерческого грузооборота транспорта имеет следующий вид:
Из этой
модели следует, что основными факторами, влияющими на динамику коммерческого
грузооборота транспорта в среднесрочной перспективе, являются реальные доходы
населения (rinc), реальный обменный курс (er) и индекс тарифной
политики естественных монополий (rmon).
Эти выводы объясняются тем, что реальные доходы населения являются важнейшим
фактором макроэкономической конъюнктуры, определяющим динамику агрегированного
спроса и коммерческих услуг транспорта. Индекс тарифной политики в отраслях
естественных монополий влияет на издержки предприятий реального сектора,
заставляя их корректировать реальные объемы производства, а следовательно, и
спрос на услуги транспорта. Коэффициент эластичности индекса коммерческого
грузооборота транспорта по фактору реальных доходов населения равен 0.25. Это
означает, что рост реальных доходов населения на 1% приводит к увеличению
реального объема коммерческого грузооборота транспорта на 0.25% в среднесрочной перспективе.
Коэффициент эластичности индекса коммерческого грузооборота транспорта по индексу тарифной политики в отраслях
естественных монополий равен -0.39. Это означает, что опережающий рост индекса
тарифной политики естественных монополий на 1% ведет к спаду грузооборота
транспорта на 0.39%.
Влияние
реального обменного курса на динамику коммерческого грузооборота транспорта,
отраженное в среднесрочном коэффициента эластичности -0.28, можно объяснить на
основе механизма «голландской болезни» российской экономики. Высокий уровень
мировых и экспортных цен на нефть, газ и металлы приводит к большому притоку
твердой валюты в Россию и укреплению рубля в реальном выражении относительно
доллара. Приток валюты стимулирует рост производства, прежде всего, в экспортно-ориентированных
отраслях, а также через заказы на промежуточную продукцию индуцирует рост
выпуска в технологически связанных отраслях экономики и промышленности. В
результате укрепление рубля в реальном выражении оказывается положительно
связано с ростом агрегированного выпуска и увеличением спроса на услуги
транспорта. Моделирование показателя ltransp методом OLS Выборка данных: 1997 (1) - 2004 (4)
* - значима на 5% уровне ошибки выражение в квадратных скобках – это вероятность того, что данная статистика равна нулю
ВВП Полученная модель коррекции ошибок, описывающая как среднесрочные, так и краткосрочные тенденции в динамике ВВП на интервале 1997(1)-2004(4), имеет следующий вид:
Эта эконометрическая модель позволяет выделить следующие основные факторы, влияющие на среднесрочную динамику ВВП:
Краткосрочная динамика российского ВВП зависит также от следующих факторов:
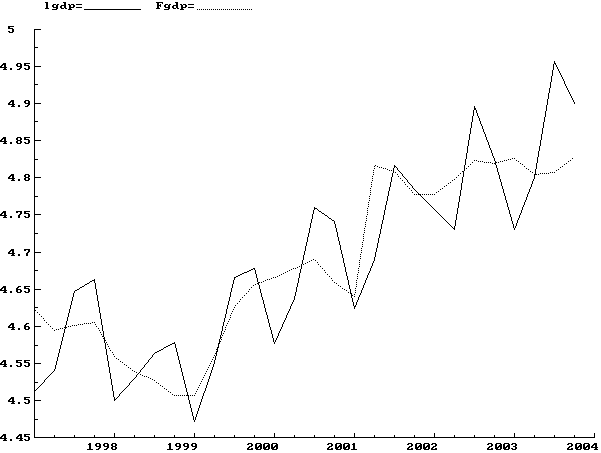
Моделирование показателя lgdp методом OLS Выборка данных: 1997 (1) - 2004 (4)
Моделирование показателя Dlgdp методом OLS Выборка данных: 1997 (1) - 2004 (4)
выражение в квадратных скобках – это вероятность того, что данная статистика равна нулю
Приложение: статистические показатели и критерии, использованные в расчетах
и оценках Все использованные методы статистического оценивания базируются на идее оценок МНК, что позволяет документировать и исследовать качество полученных регрессионных и коинтеграционных зависимостей с использованием известных статистических тестов, которые кратко описаны ниже:
** означает, что гипотеза значима на 1% уровне ошибки, * - значима на 5% уровне ошибки.
Статистические тесты качества полученной регрессионной зависимости основаны на F - статистике или Chi2 - статистике. Например, для F - статистики характерная форма представления результатов имеет вид: F(1,155)=5.0088 [0.0266] *, что означает следующее: значение F-статистики с указанным числом степеней свободы равно 5.0088; вероятность получить это значение при данном распределении равна 0.0266. Это меньше 5%, но больше 1%, отсюда значок *. В частности, все полученные эконометрические зависимости тестировались на:
Типичная форма результатов тестирования имеет следующий вид:
AR
1-3 – тест на автокорреляцию остатков высокого порядка (Breusch-Godfrey test) Если регрессионные остатки автокоррелированы, то это означает низкое качество полученной регрессионной зависимости, которую нельзя использовать для полноценного анализа и прогноза динамики исследуемого показателя. Тест Дарбина-Уотсона (DW), обычно используемый для анализа автокорреляции остатков, имеет множество недостатков, среди которых – ограниченность 1-м порядком автокорреляции. Общий тест на автокорреляцию остатков высокого порядка был предложен Бройшем и Годфри. Суть его заключается в следующем: предположим, что остатки в регрессионной зависимости описываются следующей моделью автокорреляции высокого порядка:
где «шумы» независимы и одинаково распределены с нулевым средним, .
Нулевая гипотеза заключается в том, что
Процедура
тестирования гипотезы состоит из следующих
шагов:
В дальнейших вычислениях используется значение
p=3.
Таким образом, если вычисленная статистика
F
превышает
критические пороги на уровне ошибки 5% и 1%, что отражается в символах * и **
соответственно в приведенной выше форме результатов тестирования для
AR 1-3, то
гипотеза отклоняется на уровне
5% и 1% соответственно.
Это означает, что остатки регрессионной зависимости для
исследуемого показателя автокоррелированы и желательно модифицировать
спецификацию модели для построения более качественной зависимости.
ARCH тест Этот тест был предложен для обнаружения специфичной гетероскедастичности, присущей моделям временных рядов в ситуациях, когда дисперсия ошибок прогноза варьируется от периода к периоду. Наличие авторегрессионной условной гетероскедастичности в оцениваемой регрессионной модели существенно снижает ее качество, что вызывает необходимость модификации этой модели. Более формально, пусть оцениваемая регрессионная модель имеет следующий вид:
где - независимые регрессоры, а дисперсии «шумов» варьируются от периода к периоду, т.е.
Нулевая гипотеза: . Процедура тестирования состоит из следующих шагов:
В дальнейших вычислениях используется значение p=3. Таким образом, если вычисленная статистика F превышает критические пороги на уровне ошибки 5% и 1%, что отражается в символах * и ** соответственно в приведенной выше форме результатов тестирования для ARCH, то гипотеза отклоняется на уровне 5% и 1% соответственно.
Xi2, Xi*Xj -
Тест Уайта на гетероскедастичность Этот тест был предложен для проверки общей гипотезы о наличии гетероскедастичности в исследуемой регрессионной модели, т.е. ситуации, в которой «шумы» наблюдений зависят от некоторых факторов и изменяются от наблюдения к наблюдению. Более конкретно, рассмотрим следующую регрессионную модель:
Процедура тестирования состоит из следующих шагов:
где - коэффициент
детерминации вспомогательной регрессионной модели,
df - число степеней
свободы, равное количеству регрессоров вспомогательной регрессионной модели за
исключением константы (в рассматриваемом случае
df=5). Соответственно, если вычисленная
статистика F
превышает критические пороги на уровне ошибки 5% и 1%, что отражается в
символах * и ** соответственно в приведенной выше форме результатов
тестирования для тестов Xi2 и Xi*Xj, то гипотеза отклоняется на уровне
5% и 1% соответственно.
Ошибки
спецификации модели – RESET тест Рамсея
Ошибки спецификации модели могут
повлечь за собой существенное ухудшение качества регрессионной зависимости. Для
проверки гипотезы об отсутствии ошибок спецификации Рамсеем был предложен тест
RESET
(regression specification error test), суть которого проиллюстрируем на
следующем примере. Пусть регрессионная
модель имеет вид:
Процедура тестирования
состоит из следующих шагов:
Если
значение
F оказывается значимым
на 5% или 1% уровне ошибки, то принимается гипотеза о том, что
спецификация исходной модели неверна, что отражается в символах * и **
соответственно в приведенной выше форме результатов тестирования.
Нормальность остатков (хи-квадрат тест) Тест на нормальность остатков базируется на статистике Chi2: например, Normality Chi2=2.1867[0.3351]. Это означает следующее: гипотеза нормальности регрессионных остатков в данном случае не отвергается, поскольку 5% критический уровень для статистики Chi2 равен 5.99 (или иначе, вероятность события (Chi2>2.1867) равна 0.3351, что больше 5%. * означает отклонение гипотезы нормальности на уровне 5%; ** - отклонение гипотезы нормальности на уровне 1%. Практически это часто происходит из-за влияния резко выделяющихся наблюдений, например, эффекта кризиса 1998 г. Необходимо пересмотреть спецификацию модели, включив в нее соответствующие фиктивные-переменные.
Литература Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. — М.: Юнити, 1998. Айвазян С.А., Бродский Б.Е. Макроэконометрическое моделирование: подходы, проблемы, пример эконометрической модели экономики России. ЭММ, 2005.
Cuthbertson
K., Hall S., Taylor M. Applied Econometric Techniques. Harvester, L., 1992
Green
W. H. Econometric Analysis, 2nd ed., MacMillan, N.Y., 1993.
Gujarati
D. N. Basic Econometrics, 3rd ed., McGraw-Hill, N.Y., 1995. Бродский Б.Е. Лекции по макроэкономике переходного периода. М. ГУ-ВШЭ, 2005.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Контакты: ЦЭМИ РАН 117418, Москва, Нахимовский проспект, 47, комната 1110 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
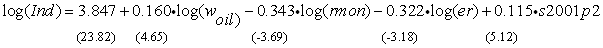 ,
,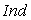 - базовый индекс промышленного производства в России;
- базовый индекс промышленного производства в России;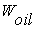 -
экспортная цена на сырую нефть;
-
экспортная цена на сырую нефть;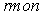 - индекс
тарифной политики естественных монополий, рассчитываемый как
отношение базового индекса цен на электроэнергию для конечных
потребителей к базовому индексу потребительских цен, т.е.
- индекс
тарифной политики естественных монополий, рассчитываемый как
отношение базового индекса цен на электроэнергию для конечных
потребителей к базовому индексу потребительских цен, т.е.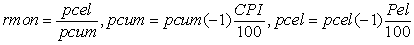 ,
,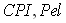 -
квартальный индекс потребительских цен и индекс цен на
электроэнергию для конечных потребителей соответственно;
-
квартальный индекс потребительских цен и индекс цен на
электроэнергию для конечных потребителей соответственно;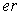 -
отношение номинального обменного курса доллара к базовому индексу
потребительских цен, т.е.
-
отношение номинального обменного курса доллара к базовому индексу
потребительских цен, т.е.
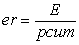 ;
;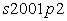 -
фиктивная переменная налоговой политики, равная нулю до 2001(2) и единице после
этого момента, соответствующая введению в действие основных статей
нового Налогового Кодекса в 2001-2002 гг.
-
фиктивная переменная налоговой политики, равная нулю до 2001(2) и единице после
этого момента, соответствующая введению в действие основных статей
нового Налогового Кодекса в 2001-2002 гг.
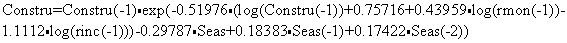
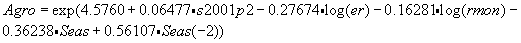
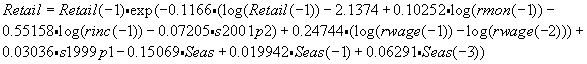
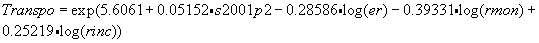
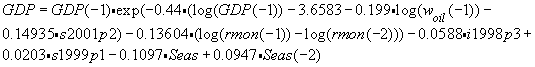
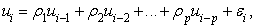
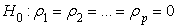 .
. 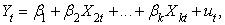
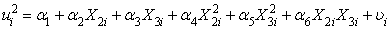
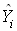 и коэффициент
детерминации.
и коэффициент
детерминации.